Traveling Salesman Problem
-Projekti-
Website maintained by ntrifunovic Theme by mattgraham modified by ntrifunovic
Traveling Salesman Problem (TSP)
Repostory: https://github.com/ntrifunovic/TSP
Implementacija nekoliko heuristika za problem trgovackog putnika i njihova vizuelizcija. Jezik koriscen za izradu projekta je python.
Screen Shots

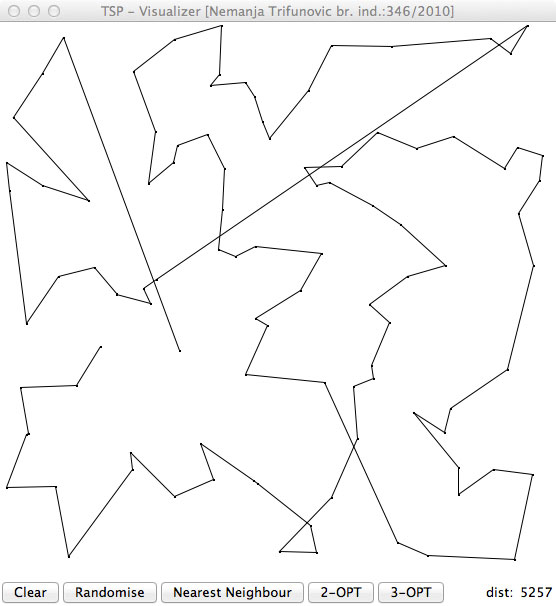

Izvorni Kod
#!/usr/bin/python from Tkinter import * from random import * from math import sqrt points = [] size = 550 def click(event): draw_point(event.x, event.y) points.append((event.x, event.y)) def draw_point(x, y): c.create_oval(x, y, x+1, y+1, fill="black", tags = "point") def draw_points(): c.delete("point", "line"); map(lambda point: draw_point(point[0], point[1]), points) def draw_line(): c.delete("line") c.create_line(points, tags="line") def clear(): global points points = [] c.delete("point", "line"); def randomise(): global points points = [] for i in range(100): points.append((randint(1,size), randint(1,size))) draw_points() def nearest_neighbour_algorithm(points): if len(points) == 0: return [] #current = choice(points) current = points[0] nnpoints = [current] points.remove(current) while len(points) > 0: next = points[0] for point in points: if dist(current, point) < dist(current, next): next = point nnpoints.append(next) points.remove(next) current = next return nnpoints def two_opt(points): for i in range(len(points) - 1): for j in range(i + 2, len(points) - 1): if dist(points[i], points[i+1]) + dist(points[j], points[j+1]) > dist(points[i], points[j]) + dist(points[i+1], points[j+1]): points[i+1:j+1] = reversed(points[i+1:j+1]) return points def three_opt(points): for i in range(len(points) - 1): for j in range(i + 2, len(points) - 1): for k in range(j + 2, len(points) - 1): way = 0 current = dist(points[i], points[i+1]) + dist(points[j], points[j+1]) + dist(points[k], points[k+1]) if current > dist(points[i], points[i+1]) + dist(points[j], points[k]) + dist(points[j+1], points[k+1]): current = dist(points[i], points[i+1]) + dist(points[j], points[k]) + dist(points[j+1], points[k+1]) way = 1 if current > dist(points[i], points[j]) + dist(points[i+1], points[j+1]) + dist(points[k], points[k+1]): current = dist(points[i], points[j]) + dist(points[i+1], points[j+1]) + dist(points[k], points[k+1]) way = 2 if current > dist(points[i], points[j]) + dist(points[i+1], points[k]) + dist(points[j+1], points[k+1]): current = dist(points[i], points[j]) + dist(points[i+1], points[k]) + dist(points[j+1], points[k+1]) way = 3 if current > dist(points[i], points[j+1]) + dist(points[k], points[i+1]) + dist(points[j], points[k+1]): current = dist(points[i], points[j+1]) + dist(points[k], points[i+1]) + dist(points[j], points[k+1]) way = 4 if current > dist(points[i], points[j+1]) + dist(points[k], points[j]) + dist(points[i+1], points[k+1]): current = dist(points[i], points[j+1]) + dist(points[k], points[j]) + dist(points[i+1], points[k+1]) way = 5 if current > dist(points[i], points[k]) + dist(points[j+1], points[i+1]) + dist(points[j], points[k+1]): current = dist(points[i], points[k]) + dist(points[k], points[i+1]) + dist(points[j], points[k+1]) way = 6 if current > dist(points[i], points[k]) + dist(points[j+1], points[j]) + dist(points[i+1], points[k+1]): current = dist(points[i], points[k]) + dist(points[j+1], points[j]) + dist(points[i+1], points[k+1]) way = 7 if way == 1: points[j+1:k+1] = reversed(points[j+1:k+1]) elif way == 2: points[i+1:j+1]= reversed(points[i+1:j+1]) elif way == 3: points[i+1:j+1],points[j+1:k+1] = reversed(points[i+1:j+1]),reversed(points[j+1:k+1]) elif way == 4: points = points[:i+1] + points[j+1:k+1] + points[i+1:j+1] + points[k+1:] elif way == 5: temp = points[:i+1] + points[j+1:k+1] temp += reversed(points[i+1:j+1]) temp += points[k+1:] points = temp elif way == 6: temp = points[:i+1] temp += reversed(points[j+1:k+1]) temp += points[i+1:j+1] temp += points[k+1:] points = temp elif way == 7: temp = points[:i+1] temp += reversed(points[j+1:k+1]) temp += reversed(points[i+1:j+1]) temp += points[k+1:] points = temp return points def dist(a, b): return sqrt(pow(a[0] - b[0], 2) + pow(a[1] - b[1], 2)) def distance(points): if len(points) == 0: return 0 distance = 0 for i in range(len(points) - 1): distance += dist(points[i], points[i + 1]) return distance def optimisation_click(algorithm): global points points = algorithm(points) draw_line() v.set(int(distance(points))) root = Tk() root.title("TSP - Visualizer [Nemanja Trifunovic br. ind.:346/2010]") root.resizable(0,0) c = Canvas(root, bg="white", width = size, height = size) c.configure(cursor="crosshair") c.pack() c.bind("<Button-1>", click) Button(root, text = "Clear", command = clear).pack(side = LEFT) Button(root, text = "Randomise", command = randomise).pack(side = LEFT) Button(root, text = "Nearest Neighbour", command = lambda : optimisation_click(nearest_neighbour_algorithm)).pack(side = LEFT) Button(root, text = "2-OPT", command = lambda : optimisation_click(two_opt)).pack(side = LEFT) Button(root, text = "3-OPT", command = lambda : optimisation_click(three_opt)).pack(side = LEFT) v = IntVar() Label(root, textvariable = v).pack(side = RIGHT) Label(root, text = "dist:").pack(side = RIGHT) root.mainloop()
comments powered by Disqus